이번 포스터에서는 강화학습 알고리즘 중 정책반복을 구현해 보겠습니다.
저번 포스터에서는 미로 안을 무작위로 이동하는 정책을 구현했었습니다. 이번에는 에이전트가 바로 목표로 향하도록 정책을 학습해 보겠습니다.
정책 반복과 가치반복
정책 반복 : 지금까지 행했던 액션(행동)에 대해 가치를 매겨, 가치가 높은 행동들을 중시하도록 정책을 수정.
가치 반복 : 목표 지점부터 거슬러 올라가 목표지점과 가까운 상태로 유도하는 방법.
쉽게 말해 정책 반복은 행동에 대해 가치를 매겨, 가치가 높은 행동들을 하게 하는 방법입니다. 그와 대조되게 가치 반복은 상태에 대해 가치를 매겨, 가치가 높은 상태로 가도록 유도하는 방법입니다.
그리고 오늘 소개할 정책 경사 알고리즘은 정책 반복 알고리즘의 한 종류입니다.
미로구현
앞선 포스터와 동일하게 미로를 구현해 줍니다.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
fig = plt.figure(figsize=(5,5)) # 전체 화면 크기를 설정해 준다.
ax = plt.gca() # 화면의 x, y 축을 받아온다.
ax.set_xlim(0,3) # 위에서 받은 x 축의 범위는 0~3까지이다.
ax.set_ylim(0,3) # 위에서 받은 y 축의 범위는 0~3까지이다.
# 미로를 구성하는 빨간 줄을 그어준다
plt.plot([1,1], [0,1], color='red', linewidth=2)
plt.plot([1,2], [2,2], color='red', linewidth=2)
plt.plot([2,2], [2,1], color='red', linewidth=2)
plt.plot([2,3], [1,1], color='red', linewidth=2)
# 각 상태(State)를 지정해 주고 그 위에 상태들을 텍스트로 표기해 준다.
plt.text(0.5, 2.5, 'S0', size=14, ha='center')
plt.text(1.5, 2.5, 'S1', size=14, ha='center')
plt.text(2.5, 2.5, 'S2', size=14, ha='center')
plt.text(0.5, 1.5, 'S3', size=14, ha='center')
plt.text(1.5, 1.5, 'S4', size=14, ha='center')
plt.text(2.5, 1.5, 'S5', size=14, ha='center')
plt.text(0.5, 0.5, 'S6', size=14, ha='center')
plt.text(1.5, 0.5, 'S7', size=14, ha='center')
plt.text(2.5, 0.5, 'S8', size=14, ha='center')
# 시작위치와 목적지를 지정해 주고 그 위에 텍스트로 표기해 준다.
plt.text(0.5, 2.3, 'Start', ha='center')
plt.text(2.5, 0.3, 'Goal', ha='center')
# 그림의 x, y 축의 속성을 설정해 준다.
plt.tick_params(axis='both', which='both', bottom=False, top=False, labelbottom=False, right=False, left=False, labelleft=False)
# 미로 찾기에서의 에이전트인 원을 그려준다
circle, = ax.plot([0.5], [2.5], marker="o", color='g', markersize=60)
# (실제로는 plot()이 라인들의 리스트를 반환하기 때문에 여기선 circle 뒤에 콤마를 붙였다)
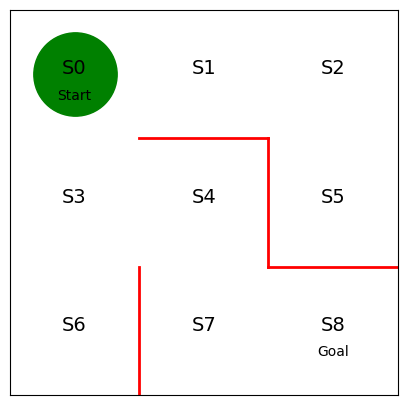
위의 코드를 실행하면 위 사진과 같은 결과를 얻을 수 있습니다.
# 각 상태별 에이전트의 행동 규칙 ( [a, b, c, d] )
theta_0 = np.array([[np.nan, 1, 1, np.nan], # S0
[np.nan, 1, np.nan, 1], # S1
[np.nan, np.nan, 1, 1], # S2
[1, 1, 1, np.nan], # S3
[np.nan, np.nan, 1, 1], # S4
[1, np.nan, np.nan, np.nan], # S5
[1, np.nan, np.nan, np.nan], # S6
[1, 1, np.nan, np.nan], # S7
])
# S8의 경우 목적지이기에 행동이 필요 없다.
마지막으로 초기 정책을 설정해 주는 것으로 준비는 끝이 납니다.
softmax로 초기 정책 비율을 계산
def softmax_convert_into_pi_from_theta(theta):
'''비율 계산을 softmax 함수로 구현한다.'''
beta = 1.0 # 역온도(incerse temperature) : 역온도가 작아질수록 행동이 무작위로 선택
[m, n] = theta.shape # theta의 행렬 크기를 구함
pi = np.zeros((m, n))
exp_theta = np.exp(beta * theta) # theta를 exp(beta * theta)로 변환
for i in range (0, m):
# pi [i, :] = theta [i, :] / np.nansum(theta[i, :]) # 단순 비율을 계산하는 코드
pi[i, :] = exp_theta[i, :] / np.nansum(exp_theta[i, :]) # softmax로 계산하는 코드
pi = np.nan_to_num(pi) # nan을 0으로 변환
return pi
코드로 softmax함수를 구현한 코드이다. theta의 계수 beta는 역온도로, 역온도가 작아질수록 행동이 무작위로 선택된다.
# 초기 정책 pi_0을 계산
pi_0 = softmax_convert_into_pi_from_theta(theta_0)
print(pi_0)
[[0. 0.5 0.5 0. ]
[0. 0.5 0. 0.5 ]
[0. 0. 0.5 0.5 ]
[0.33333333 0.33333333 0.33333333 0. ]
[0. 0. 0.5 0.5 ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.5 0.5 0. 0. ]]
초기 정책 pi_0을 계산한 결과는 위와 같다.
def get_action_and_next_s(pi, s):
direction = ["up", "right", "down", "left"]
next_direction = np.random.choice(direction, p=pi[s, :])
if next_direction == "up":
action = 0
S_next = s - 3
elif next_direction == "right":
action = 1
S_next = s + 1
elif next_direction == "down":
action = 2
S_next = s + 3
elif next_direction == "left":
action = 3
S_next = s - 1
return [action, S_next]
앞 포스터와 마찬가지로 위의 코드를 사용하여 다음 상태를 알 수 있다. 하지만 앞 포스터에서는 상태만 리턴으로 받았다면, 여기서는 정책 경사 알고리즘을 사용하기 위해 해당 액션도 함께 리턴으로 받는다.
def goal_maze_ret_s_a(pi):
s = 0
s_a_history = [[0, np.nan]] # 에이전트의 행동 및 상태의 히스토리를 기록하는 리스트
while True:
[action, next_S] = get_action_and_next_s(pi, s)
s_a_history[-1][1] = action # 현재 상태(마지막이므로 인덱스가 -1)를 히스토리에 추가 s_a_history.append([next_S, np.nan])
#다음 상태를 히스토리에 추가, 행동은 아직 알 수 없으므로 nan으로 둔다
if next_S == 8:
break
else:
s = next_S
return s_a_history
s_a_history = goal_maze_ret_s_a(pi_0)
print(s_a_history)
print("목표 지점까지 걸린 단계 수는" + " " + str(len(s_a_history) - 1) + "입니다")
위의 코드를 실행하면 초기 정책을 사용하여 목표에 이르기까지의 단계가 출력됩니다.

앞 포스터와 다르게 지금 얻은 결과는 [선택한 액션, 다음 상태] 형태의 리스트입니다.
정책 경사 알고리즘으로 정책 수정
# theta를 수정하는 함수
def update_theta(theta, pi, s_a_history):
eta = 0.1 # 학습률
T = len(s_a_history) - 1 # 목표지점까지 걸린 단계 수
[m, n] = theta.shape
delta_theta = theta.copy() # delta theta를 구할 준비, 포인터 참조이므로 delta_theta = theta로는 안 됨
# delth_theta를 소요 단위로 계산
for i in range(0, m):
for j in range(0, n):
if not(np.isnan(theta[i, j])): # theta가 nan이 아닌 경우
SA_i = [SA for SA in s_a_history if SA[0] == i]
# 히스토리에서 상태 i인 것만 모아 오는 리스트 컴프리헨션
SA_ij = [SA for SA in s_a_history if SA == [i,j]]
# 상태 i에서 행동 j를 취한 경우만 모음
N_i = len(SA_i) # 상태 i에서 모든 행동을 취한 횟수
N_ij = len(SA_ij) # 상태 i에서 행동 j를 취한 횟수
delta_theta[i, j] = (N_ij - pi[i, j] * N_i) / T
new_theta = theta + eta * delta_theta
return new_theta
위에 코드를 실행시키면 파라미터 theta가 수정되고, 이에 따라 정책 pi가 수정된다. 수정된 결과는 아래와 같다
[[0. 0.50079787 0.49920213 0. ]
[0. 0.50079787 0. 0.49920213]
[0. 0. 0.50212765 0.49787235]
[0.33392433 0.33356928 0.33250639 0. ]
[0. 0. 0.5 0.5 ]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.5 0.5 0. 0. ]]
이제 미로를 빠져나오도록 반복문을 구현해 준다.
# 정책 경사 알고리즘으로 미로 빠져나오기
stop_epsilon = 10**-4 # 정책의 변화가 10^4보다 작아지면 학습 종료
theta = theta_0
pi = pi_0
is_continue = True
count = 1
while is_continue:
s_a_history = goal_maze_ret_s_a(pi)
new_theta = update_theta(theta, pi, s_a_history)
new_pi = softmax_convert_into_pi_from_theta(new_theta)
print(np.sum(np.abs(new_pi - pi)))
print("목표 지점까지 걸린 단계 수는" + " " + str(len(s_a_history) - 1) + "입니다")
if np.sum(np.abs(new_pi - pi)) < stop_epsilon:
is_continue = False
else:
theta = new_theta
pi = new_pi
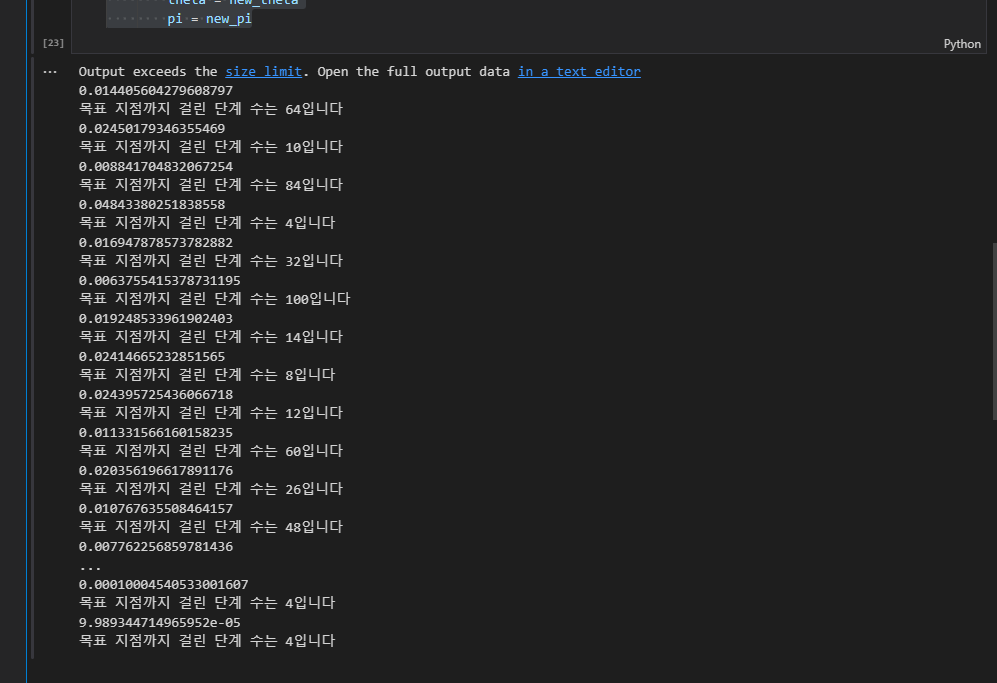
마지막으로 학습이 완료된 정책을 확인해 보면
[[0. 0.016 0.984 0. ]
[0. 0.244 0. 0.756]
[0. 0. 0.463 0.537]
[0.011 0.977 0.012 0. ]
[0. 0. 0.987 0.013]
[1. 0. 0. 0. ]
[1. 0. 0. 0. ]
[0.013 0.987 0. 0. ]]
위와 같이 수정이 되었습니다.

이번 포스터에서는 정책 경사 알고리즘을 사용하여 정책을 학습하였습니다. 다음 포스트에서는 가치반복 알고리즘을 구현해 보도록 하겠습니다.
'황민규 > 강화학습 예제' 카테고리의 다른 글
| Dynamic Programming (0) | 2023.04.11 |
|---|---|
| A2C 알고리즘[#2] (0) | 2023.04.04 |
| A2C 알고리즘[#1] (0) | 2023.03.28 |
| 강화학습 미로찾기 구현(#1) (0) | 2023.03.07 |



