이전 글에 이어서 Loss를 최소화하기 위한 Back-propagation(Backward-propagation) 과정에 대해서 설명하겠습니다.

위의 Loss 함수를 최소화해야 합니다. 수학에서는 함수의 최솟값을 구하기 위해서 미분을 하고 미분한 값의 부호가 (-)에서 (+)로 바뀌는 지점을 찾습니다. 이런 지점을 '극소점'이라고 부르며 이 극소점 중에서 가장 함수의 값이 작은 지점을 '최소점'이라고 부릅니다.
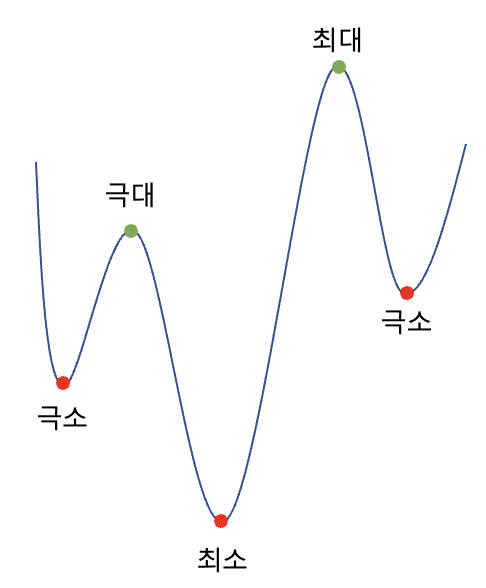
위의 그래프는 Loss function의 그래프이며 이 함수를 미분하여 함수가 '최소'가 되는 지점을 찾아가는 것이 Machine Learning에서의 '학습'입니다. 더 정확히 말하면 이 '학습'이란 Loss function을 최소로 만드는 weight parameters 즉, 이전 글에서 다뤘던 weight vector인 최적의 W를 찾는 과정입니다.


위의 그림 Part 1에서 input X에 곱해지는 weight W의 최적값을 찾는 과정을 뜻합니다. 이 과정을 위해서 Backpropagation(Backward-propagation)이라는 방법이 사용됩니다.
II. Backward-propagation
Backpropagation은 이전글의 Forward-propagation을 거꾸로 거슬러 올라가면서 최종 Loss function에 어떤 weight parameter가 어느 정도의 영향을 미치는지 각각 계산하여 그 영향력을 반영하여 weight parameter값을 Loss가 최소화하는 방향으로 update 합니다.

위의 식에서 alpha값은 learning rate로 얼만큼의 비율로 weight를 업데이트할 것인지를 결정하는 hyperparameter(모델을 설계하는 사람이 임의로 정하는 값)입니다. 이 [alpha값]을 [예측값 a와 실제값 y사이의 Loss에 w가 얼마의 영향을 미치는지 계산한 Gradient값]에 곱하여 원래 w에 빼서 update 해줍니다.
이 공식의 Gradient값을 구하기 위해서 Chain Rule을 사용합니다.

z가 y에 대한 식으로 나타내지고, y는 x에 대한 식으로 나타낼 수 있다면, z에 대한 x의 미분계수 dz/dx를 위와 같이 나타낼 수 있습니다. 이를 이용해 Loss 값의 w에 대한 (편) 미분계수는 아래와 같이 계산할 수 있습니다.

① Loss 값은 예측값 a에 대한 식으로 나타낼 수 있고, ② a는 z에 대한 식으로 나타낼 수 있으며, ③ z는 w에 대한 식으로 나타낼 수 있으므로 Chain Rule을 적용하여 위와 같이 계산할 수 있습니다.
1. Partial Derivative of Loss function (①)
먼저 Loss function(L)을 예측값 a에 대한 식으로 나타낼 수 있으므로 L의 a에 대한 편미분계수를 구합니다.

2. Partial Derivative of activation function (②)
Activation function(a = 예측값)을 Linear Equation z에 대한 식으로 나타낼 수 있으므로 a의 z에 대한 편미분계수를 구합니다.

3. Partial Derivative of Linear Equation (③)
Linear Equation(=z)을 weight w에 대한 식으로 나타낼 수 있으므로 z의 w에 대한 편미분계수를 구합니다.

4. Calculation by using Chain Rule
위의 1, 2, 3에서 계산한 값을 Chain Rule을 이용하여 계산한 최종 Gradient는 다음과 같습니다.

5. Weights Update
4에서 계산한 Gradient에 learning rate alpha를 곱하여 weight w를 update 해줍니다.

이전에 우리는 W vector를 input vector X와 dot product 연산을 통해 계산했으니 이걸 weights update 단계에 적용하면 다음과 같이 나타낼 수 있습니다.

각 weight parameters를 위와 같이 update 하고 이런 1~5의 과정을 Back-propagation이라고 부릅니다.


